102. Drawing fractals

Fractal recipes

So where should we start if we want to draw a fractal? As I already mentioned in the introductory post, the defining characteristic of any fractal is the recipe (or rule) that is used to generate it. In general there can be multiple such generator rules and they can even vary over time, but to keep things simple for the purposes of this post we are only going to consider fractals that are defined in terms of a single unchanging rule. Furthermore, for us to be able to (at least theoretically) build an infinitely detailed fractal the generator rule we choose must always remain applicable. This means that whatever we choose as the basic building blocks of our fractal – whether it be geometric objects such as points, lines, or triangles, or whether it be physical objects such as atoms, cells, or LEGO® blocks – the rule must be able to operate on those components. We wish to avoid a situation where a rule that turns apples into oranges will run out of apples since this will result in an static and thus permanent end state.

Which brings us to the next thing we need — a recipe needs ingredients! In the digital space it is difficult to work with actual apples and oranges and besides, in terms of visualization it is best if we stick with geometric objects for now. The upside of this is that provided our rules are not overly analytical it is relatively easy to sketch out the analog fractal shapes on paper. The fractal curves we'll go through are all composed of just lines (or line segments to be pedantic) and the rules which operate on those lines will all be of the form "replace each line with X", where X is some new arrangement of lines. Properly examining the versatility of the last curve will require us to also utilize triangles and points.

There's still just one minor problem though. We need to start somewhere, but what should our starting state look like? We can't start from nothing since otherwise our rule will have nothing to work on, but on the other hand everything else feels a bit arbitrary. For fractal curves, starting out with just a single line is arguably the least arbitrary and therefore the most suitable option. In general, starting with a single building block (whatever it may be) is usually wisest, and once you get a feeling for how the rule behaves you are better equipped to try out other seed states. Note that it is possible to think of the arbitrary initial state as a single-use generator rule in its own right which operates on "empty", and come to think of it, assuming an empty starting state is also just another arbitrary choice. But before things get too metaphysical, let's get on with the fractals. First a demo, then some words.

Koch curve

In a paper published in 1904 a Swedish mathematician by the name of Helge von Koch described a peculiar curve which although continuous did not have well-defined tangents. In the paper he references a similar curve discovered by Karl Weierstrass in 1872¹ and voices certain objections regarding it. In his words the analytic function "hides the geometric nature of the resulting curve" making it non-obvious why the curve is not differentiable. To address these perceived shortcomings he introduced his own curve which, instead of being analytical, is constructed geometrically. Over a hundred years later, the Koch curve still carries his name.

Koch pattern

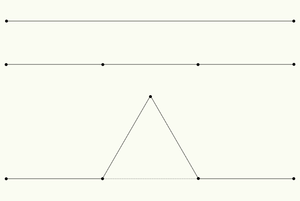
Instead of going through Koch's (very rigorous) description I shall summarize its governing rule like this: First, divide each existing line into three new lines of equal length, then imagine an equilateral triangle with its base coinciding with the one in the middle, add the two sides of the triangle as new lines while removing the base. This recipe has the effect of turning each line into four smaller lines. Since each of the new lines is equal in length to a third of the original this means that the curve grows by an extra third in length each time we perform the subdivision – after an infinite number of steps the curve has infinite length. As a consequence of the growth rate the fractal dimension of the curve turns out to be approximately 1.26186 — or more precisely, the natural logarithm of four divided by the natural logarithm of three. You can play around with the first seven iterations of the curve using the demo. After the seventh iteration the added detail becomes so miniscule that we run out of display resolution.

If instead of a line we decide to start things off with a triangle the three independent Koch curves will (under iteration) begin to resemble a happy little snowflake. Although this happens to highlight an ambiguity in the way we formulated our rule. When we add the triangular point we have to decide on which side of the line we place it. In the case of the curve we can describe the desired behaviour in the following way. Imagine that the curve divides the plane into two halves which we will arbitrarily label In and Out. This allows us to say that the extrusion should always happen away from Out and towards In — whatever this direction happens to be in the local context. In a similar manner we decree that the edges of the Koch snowflake should always extend away from the enclosed Out at the center. The opposite decision results in the shape labeled the Koch antisnowflake.

You can cycle through these different shapes (in the order of introduction) by simply tapping on the animation. The fourth shape is something that I added on a whim while implementing this demo. The extrusion pattern is the same as before, but the extrusion directions alternate between iterations. Because of the shape that results I thought "Koch molecule" would be a fitting name.

Minkowski sausage

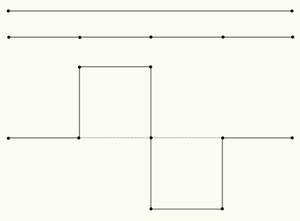
The fifth fractal recipe shown is the delightfully named Minkowski sausage, also known as the quadratic type 2 Koch curve. Again we start with a single line segment, but this time the generator rule goes something like this: First, divide each existing line into four new lines of equal length, then imagine two squares (extruded in opposite directions) with their bases coinciding with the two newly created middle segments, and again remove these baselines. This process turns each line into eight new lines (resembling a square wave) each a fourth of the length of the original therefore doubling the length of the curve with each iteration. This results in the sausage being one-and-a-half dimensional, fractally speaking. Although the newly perpendicular line in the middle could be treated as a single line it would not result in the sausage-like shape. Instead we treat it as two separate lines for the purposes of further subdivisions.

Minkowski pattern

Of course, nothing prevents us from seeing what would happen if we did treat it as a single longer line. While the dimensional properties of the fractal remain unchanged its shape changes noticeably and it becomes much more squarish. Another neat detail is that now the individual lines are no longer of equal length. As we iterate the shape further the relative difference between the shortest and the longest individual lines within the curve keep doubling! Visually this gives the impression of the pattern kind of "spiraling into" its many centers, although that's just my impression. This curve might have a more commonly used name, but since I implemented it quite by (happy) accident I'm not aware of any.

Sierpinski triangle

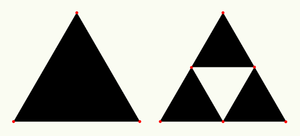
The last fractal curve we'll look into is slightly different and you can probably see why. Although it is constructed in the same manner as the previous curves as we recurse further the lines appear to get replaced by triangles! Indeed we could just as well formulate the fractal in the following way: (1) start with an equilateral triangle, (2) subdivide it into four smaller triangles of equal size and shape (each having fourth the the area of the original), repeat from step #2 for the new triangles. In both cases the fractal shape that emerges is the same. I'll leave it to you to figure out the corresponding curve rule.

Sierpinski pattern

The two alternate descriptions give us two ways to derive the fractal dimension of the shape. When built from lines, each subdivision increases the total length of the curve by a factor of ³⁄₂. When built from triangles, doubling the size of the shape is equivalent to making two copies of the original triangle thus tripling the total area. When expressed more formally, this implies that 2^D equals three, where D is the fractal dimension. Solving for D reveals it to be equal to approximately 1.58496 — more precisely, the natural logarithm of three divided by the natural logarithm of two. If we replace the triangles with tetrahedrons (ie. pyramids) it is easy to imagine how a three-dimensional version – the Sierpinski pyramid – could work. Funnily enough the Haussdorf dimension of this (topologically three-dimensional) fractal pyramid is exactly two! Carrying on in the same vein allows us to derive Sierpinski fractals of arbitrarily high dimensionality, but visualizing them causes some difficulties which we should like to avoid for now. More on higher dimensions once we get to Buddhabrot.

There are also weirder ways to generate the Sierpinski triangle. One involves combining cellular automata and the exclusive-or binary operator in the form of Rule 90. The world of cellular automata is so vast that I can't do it justice right now, but I recommend reading up on John Conway's Game of Life (for zero players!) if you haven't heard of it before. In our context it is enough to know that cellular automata also work in terms of pattern replacement rules which operate on groups of some fundamental units (usually bits). Perhaps an even stranger way to produce the Sierpinski triangle requires us to play with chaos.

Chaos games

Given the three corners of an initial equilateral triangle the Sierpinski chaos game goes like this: (1) randomly pick a reference point within the triangle, (2) then randomly pick one of the three corners of the triangle, (3) add a new point halfway between the corner and the reference point, (4) make the new point the reference point and repeat from #2. Astonishingly as we keep adding more and more points the overall shape begins to resemble the Sierpinski triangle. Despite being driven by random chance the placement pattern stabilizes remarkably quickly and even with just a few hundred points the overall shape begins to emerge. For reference, the last iteration shown by the demo has a total of 12'000 points.

Somewhat surprisingly then, if we try the same mechanism with the four corners of a square we get just uniform noise and no fractal pattern emerges. In fact, the uniformity seems more like the norm to which the chaotic Sierpinski is just a remarkable exception. All is not lost though, as introducing additional constraints allows us to restore the roughness. Suppose that when randomly picking the corner we simply avoid picking the same corner we picked last time. Now the pattern that appears is once again fractal and would actually look pretty neat on a rug! When we add another corner and switch to a pentagon we could again do without any extra conditions, but the fractal shape that results is so delicate that we need ten times more points before it starts filling out. When we apply the slightly more restrictive square rule to the pentagon the fractal structure is much more apparent.

Another option is to vary the distance factor instead of (or in addition to) avoiding corner reuse. Instead of jumping half the distance we could jump a third or fourth of the way, but again we must choose wisely. Combining either of these factors with a triangle results in more or less uniform noise, but a factor of ⅔ gets us something resembling the Sierpinski pattern. The last fractal shown by the demo is again based on a pentagon, but this time the distance factor is the inverse of the golden ratio — or approximately 0.618034. I'd wager that fractal-generating factors can be found for all regular polygons, but I know of no rigorous proofs.

On with the show

While producing fractals by means of descriptive rules is certainly possible – both manually and programmatically (as evidenced by the demo) – applying them in the latter case can be relatively cumbersome. Also, as long as we choose to limit ourselves to just a single generator rule there is a definite limit to what we can achieve in visual terms. We would also need to improve our methods somewhat to be able to draw something like the Hilbert curve mentioned in the previous post. Instead of taking things in that direction though, it sure would be great if we could somehow combine the analytic approach of Weierstrass with the geometric overtones of Koch. Fortunately, modern mathematics offers us exactly the tools we are after, but first we need to learn ► the Numbers.