103. The Numbers

Motivation

While it is perfectly possible to draw fractals using purely geometric rules it only gets you so far. If we wish to utilize the immense computational capabilities of modern day computers in our fractal explorations we will need programmable rules that can be run at least somewhat efficiently on real-world hardware. And as things stand now, computers are very fast at figuring out things like "what is A + B?", but not nearly as fast at carrying out higher-level tasks like "find every straight line in the picture and replace it with this shape". The effect of the latter visual rule can of course be replicated as an equivalent and more efficient computational task, but accomplishing that still requires us to translate – or optimally, reimplement – our fractal-generating rules in the grammar of computational language.

The simple numbers

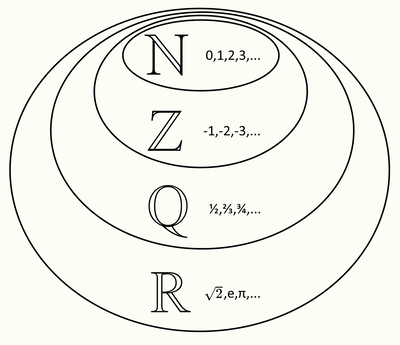
Since arithmetic is the native language of computers it is only natural that we should try to describe our fractal rules as mathematical operations — as additions, multiplications, and so on. And of course, we also need some numbers on which to perform these operations. What most of us probably think of when we hear the word 'numbers' are the numeral symbols themselves and their combinations. I myself am most familiar with the so-called Arabic numerals going from 0 to 9. While there are many ways of combining these symbols you are probably most familiar with the decimal numeral system (also known as base-10). However, the title of this post does not refer to those numbers. We are more interested in the groups of actual mathematical objects which are merely represented (in a myriad different forms) in spoken and written human languages. The obvious place to start our abstract journey are the natural numbers (N) also known as counting numbers. An infinite series of numbers you can use to count sheep when trying to fall asleep. Rest assured that you will doze off before running out of those numbers.

Although there's an infinite number of them, the natural numbers are quite restricted in terms of what we can do with them. We can add them together, we can do multiplications, and we can even subtract them to a limited degree. Once we try to subtract something from zero though it becomes obvious that we need more numbers. Adding negative numbers into the mix grows our already infinite set of numbers to include also the negative infinity, and all the numbers leading up (or down?) to it. Now we have a nice self-contained space of integers (Z) to play around in. But still we want more! We want to be able to undo our multiplications and so we go ahead and invent division. This gets us the set of all rational numbers (Q) representable as ratios of two integers (like ½). Now the rather awkward gaps between our numbers have become infinitely smaller and yet somehow more pronounced and irritating. There is also the annoyance of irrational numbers — numbers which cannot be represented as the ratios of two integers. The most famous of which is probably π¹.

By combining rational numbers with irrational numbers we end up with the so-called real numbers (R). That's basically all the numbers that can be represented by finite or infinite sequences of numerals separated by a decimal point where applicable. Although this decimal representation is practical, I personally feel that continued fractions provide a more elegant representation, but more on those later. In any case, our new set includes numbers like 19.99 (which can also be represented as a rational number) as well as numbers that start off as 3.14159265358979323846... while continuing forever. Real numbers and their associated operators allow us almost unlimited freedom, but only almost. Even though the real numbers are uncountably infinite they are still only one-dimensional and a number line is not that much to look at. Although we can cheat a bit and still draw interesting two-dimensional pictures with just the real numbers we can do much better if we simply keep expanding our concept of numbers!

Matryoshka numbers

Each new number system we have introduced up until this point has been a superset of the previous one — meaning that all natural numbers are integers, all integers as rational numbers, and so forth. So if we were to assume that real numbers are themselves just a subset of a larger number system we would be left with the question: what is their "unreal" counterpart?

What else is there?

The clue is in the name. Why are they called real numbers? Why the distinction if they are all the numbers that can possible exist? After all, there are no gaps left to fill on our number line. Adding in the irrational numbers between the rational numbers made the line completely "solid". What would it even mean if a number was unreal? As far as I can tell the prefix real owes itself to René Descartes who wanted to distinguish them from what he called imaginary numbers. Of course all numbers are imaginary in a certain sense, but Descartes meant something very specific by his description. In order to fully appreciate the motivation behind this description we need to take a short detour into square roots.

The square root (√) is a mathematical operation which answers the question: what number multiplied by itself is equal to the number I am taking a square root of? In concrete terms: two times two is four which means that two is the square root of four. Three times three is nine, so three is the square root of nine. You probably get the idea. Just like a division can undo a multiplication, the square root is the inverse operation of squaring a number — multiplying it by itself. These operations come about quite naturally if you are in the business of figuring out how to evenly divide fields into different parts: a very real problem for the geometers of ancient times. For the less ancient Descartes however, square roots were an important tool for solving polynomials — figuring out when certain mathematical constructs equal zero. Unlike his ancient colleagues he was no longer worried about the irrationality of the square root of two, but rather about the absurdity of the square root of minus one. At the time everyone knew that no ordinary number multiplied by itself could result in something negative (since two negatives always cancel out) so the whole idea of taking the square root of a negative number was thought to be nonsensical. So there was a certain unfriendly undertone that went with the term imaginary — a name which seems to have stuck. Regardless, these fictional numbers kept popping up.

It's complicated (but not really)

Eventually, just like with irrational and rational numbers, mathematicians grew used to treating imaginary numbers as just numbers. Over time everyone sort of agreed that there wasn't much point in trying to answer the nonsensical question when you could just use "the square root of minus one" as a number in its own right. Similarly to how we treat π. Whenever we have no better way to represent the number behind the symbol it sort of gains an identity of its own. Numbers like these transcend their more mundane counterparts which are mostly just derivative works. However, it is rather cumbersome to lug around "the square root of minus one" in equations so mathematicians decided to replace it with something a bit more streamlined. The abbreviation they ended up using is i, short for imaginary. Unlike π it does not lie on the real number line and instead exists in a "dimension" of its own.

The combined set of all real and imaginary numbers makes up the set of complex numbers (C). Again, the name carries with itself certain historical prejudices which many today find completely unfounded especially since the familiar arithmetic rules still apply. The only real difference is that we don't try to get rid of the imaginary numbers when they arise. So, as per our previous definition the square root of minus one² is i and since squaring cancels out an inner square root the square of the square root of minus one (or i²) is simply minus one. In short — √-1=i and (√-1)²=i²=-1. As long as that makes some sense to you the rest should follow: i plus i equals 2i, i minus 2i equals -i, i divided by 2 equals half i, and 2i times 3i equals 6i² which can be simplified to just -6.

These are just examples on imaginary numbers though. In the full complex space a number is defined in terms of its real and imaginary component which are joined together by a simple addition meaning that 3+i is a single complex number. Wrapping the numbers in parentheses allows us to treat them just like any other numerical composites. For example, multiplying (3+i) by (2-i) is the same as doing a pairwise multiplication of the components and adding them together, resulting in 6-3i+2i-i² which simplifies to 7-i. Dividing a complex number by another complex number is the only basic operation that is not quite so straightforward to express in conventional terms. Luckily we can do without division until we start considering fractal functions beyond the Mandelbrot. Knowing how complex addition and multiplication work will see us through most of the way and in the end, division is still defined to be the inverse of multiplication. Deriving this inverse becomes almost trivial if we consider a different representation.

Geometrically speaking

As alluded to earlier any complex number can be represented as a point on a two-dimensional plane with each component (real and imaginary) representing a single coordinate. In addition to this Cartesian representation an alternate polar coordinate form is sometimes used where each complex number is instead defined by its absolute value (or modulus) and argument. In other words, its distance from origin and angular direction relative to the real number line — usually symbolized by r and φ respectively. Converting between these two representations is a simple matter of ordinary geometry.

Each representation is useful in its own way. Addition and subtraction are easier to work out in the Cartesian form because you can just sum up the components individually. This is equivalent to doing additions/subtractions on 2-vectors, in case you are familiar with that sort of stuff. The so-called polar coordinate form on the other hand makes it easier to reason about multiplication and division. Instead of having to do pairwise multiplications and a subsequent simplification it turns out that you can just multiply the lengths (absolute values) and sum the angles (arguments). Since division is the inverse operation it works by dividing lengths and subtracting angles. We can even divide by zero, if we first extend our conception of the complex plane. You can play around with complex arithmetic with the small demo below where the real axis points rightward and the imaginary axis points upward. Initially, A is set equal to 1 and B is set equal to i.

You can change the values of the parameters by dragging the pins (green and red) to see how that changes the result (blue). To cycle between the different operations simply tap on the embedded button. It should become fairly obvious that complex addition can be visually thought of as a simple end-to-end joining of the parameter segments (in either order) with the sum being equal to the third side of the resulting triangle (or the diagonal of a quadrilateral). Since the subtraction can be defined equivalently as A+(-B) and it is hopefully pretty obvious how simply a negation (aka multiplication by minus one) works in the complex plane.

Multiplication in general might seem weirder at first, but you should be able to pick up on a certain input-output symmetry. Firstly, when changing the length of one of the parameters the absolute value of the result changes in equal proportion. Secondly, whenever you drag a parameter around you can see that the angle between it and the result stays fixed which is a direct consequence of how angles add up under multiplication. Consequently, when one of the parameters lies on the real number line the resulting C will always remain parallel with the second parameter, and if one of the parameters lies exactly on the imaginary axis then C will remain perpendicular to the second parameter. Note that there is a slight discontinuity whenever a parameter value crosses the negative real number line because its argument value jumps between positive and negative 180° (which can be considered to be equal³). This is merely a conceptual simplification so we don't have to deal with arbitrarily large arguments.

From our new higher-dimensional vantage point it becomes obvious that the basic arithmetic operations are transformations also when dealing with just the real number line. So the addition and subtraction you learned in school is analogous to a translation that moves numbers around on the line (or in another sense, shifts the line itself). While rotation is perhaps not a useful concept within the confines of a single dimension the scaling nature of multiplication still applies, with the zero origin acting as the pivot point. Again, it is possible to think of the multiplication as acting on the whole real number line all at once instead of operating on just single numbers — just a matter of perspective. This transformational nature of arithmetic becomes rather apparent when animating the Buddhabrot.

Conclusion

In summary, adding a complex number to another can be thought of as a translation which "moves" numbers around the complex plane. The transform analogue of complex multiplication is a combined rotation and scaling within the complex plane. Although we haven't yet touched upon how complex exponentiation works the basics you've learned thus far might allow you to gain an appreciation for what has been called (by Richard Feynman) the most beautiful formula in all of mathematics. Leonhard Euler's famous formula somewhat miraculously manages to combine complex exponentials with trigonometry. The true jewel however is the elegant identity which can be derived from the formula that manages to combine five fundamental mathematical constants (0, 1, π, e, i) using just three mathematical operations (addition, multiplication, exponentiation) — e^iπ+1=0.

That pretty much sums up all you need to know about complex numbers for now. It helps if you can follow the calculations, but really you only need to digest the core insight that although complex numbers are in essence two-dimensional it is still possible to add and multiply them together as usual. They just work — quite beautifully as we shall see. With the introductions out of the way we are now ready to start exploring the Mandelbrot set, its Julia sets, and eventually the Buddhabrot. Mathematically things start to get trickier only once we begin to consider four-dimensional rotations, but that's for later.

So what is the ► Mandelbrot set?

Appendix: Any more of them numbers?

If you picked up on the repeating pattern in the summarized history of numbers you might be tempted to ask: is there something that's beyond even complex numbers? And as you might have guessed the answer is yes, but quaternions, octonions, and other arbitrarily high-dimensional number systems (infinite-dimensional anyone?) will not be relevant for our immediate fractal purposes so I will let others do the explaining for now. For what it's worth there are also bicomplex numbers, split-complex numbers, hypercomplex as well as superreal numbers, and all sorts of other craziness to learn about, provided you're into this sort of thing.