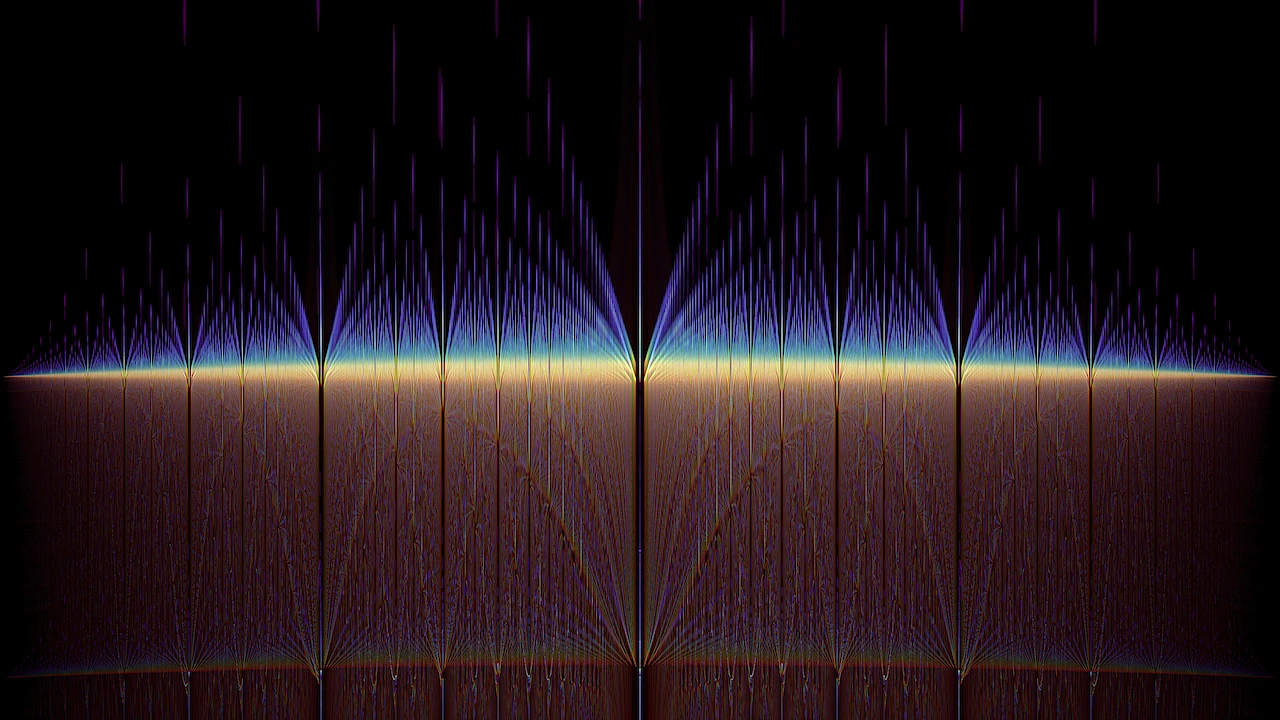
Forest for the Trees
Curiosities
Stumbled upon an intriguing pattern when exploring the fairly simple function zₙ=c+1/zₙ₋₁. Under repeated iteration the value of zₙ becomes a finite continued fraction except with complex numbers. For almost all values of c the resulting z-sequences seem to converge quickly to some fixed value of zₙ with the sole exception of a small region between and surrounding the interval -2i to +2i. Any "continued complex fraction" sequences originating near this small slice either become periodic or simply never converge.
The left side of this image coincides with c value -2i and the right side with +2i. The black gaps in the "spectrum" are the periodicity points: the larger the gap the smaller the period, with c=0 in the middle with a period of 2. Its z-sequence simply alternates between 0 and ∞ provided you define 1/0=∞ and 1/∞=0. The c-coordinates of the other gaps are more interesting. The next largest gaps to either side of 0 (in ascending periodicity) are at ±i (aka √-1), then at √-2, followed by ±iφ (golden ratio), then by √-3, after which any simple pattern becomes a bit hard to discern. As c approaches ±2i the period of the associated sequences becomes infinite: a strange kind of converge where the sequence has long stretches of relative stability punctuated by abrupt chaos, never repeating.
Between 0 and ±i the pattern of the gaps is even harder to discern. The largest of these gaps are at ±i/φ which is actually rather neat since that winks and nudges towards a nice property of the golden ratio which is 1/φ=φ-1. The seemingly strange appearance of the golden ratio and various square roots in this context might be related to the fact that they are some of the most notorious of irrational numbers. As the name implies irrational numbers are not rational — meaning that they cannot be represented as a ratio of two integers. And it just so happens that every infinite continued fraction is irrational, and every irrational number can be represented in precisely one way as an infinite continued fraction.
Using a slight 4D perspective tilt a strange wave-like pattern also becomes visible underneath the primary gap structure, the meaning of which I can only begin to guess at.